Angle Bisector Theorem Worksheet

Here, in $\delta abc$, the line ad is the angle bisector of $\angle a$. Web angle bisector theorem converse: X y p z 2 1 14) find x if m∠2 = 1 + 28 x.

Angle Bisector Theorem Side Splitter Worksheet Answers

Web an angle bisector is a straight line drawn from the vertex of a triangle to its opposite side in such a way, that it divides the angle into two equal or congruent angles. Constructions.

Quiz Worksheet Angle Bisector Theorem Proof Study —

The table below shows the statements related to internal and external angle bisector theorems as well as their converse. 13) find x if m∠2 = 4x + 5 and m∠1 = 5x − 2. In.

Angle Bisectors of Triangles Color by Number Funrithmetic

Before attempting this sheet, pupils should know how to draw and measure angles using a protractor. 13) find x if m∠2 = 4x + 5 and m∠1 = 5x − 2. What is the length.

Angle bisectorDefinition & Examples Cuemath

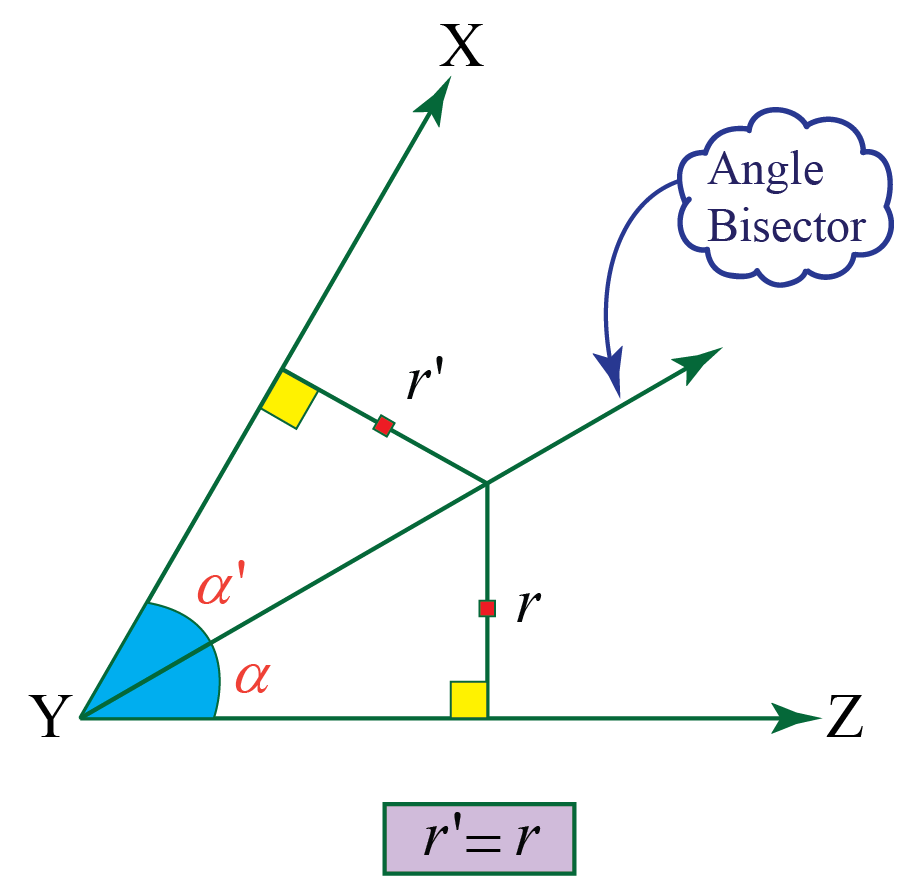
Web the angle bisectors worksheet works at ks3 and ks4 and can be completed independently by the learner or as part of your lesson. Since ad is the angle bisector of ∠a, by angle bisector.

Triangle Angle Bisector Theorem Worksheet Answers

If bd bisects the angle ∠abc, m∠abd = 3x + 15 and m∠cbd = 4x + 4, find m∠ abc. Web each figure shows a triangle with one of its angle bisectors. The following figure.

Angle Bisectors Of A Triangle Worksheet

5 = solve for x x. This principle is illustrated using a diagram with a yellow and green segment. Add both of these angles together to get the whole angle. Here, in $\delta abc$, the.

Before attempting this sheet, pupils should know how to draw and measure angles using a protractor. Add both of these angles together to get the whole angle. A and b are the lengths of the other two sides. The quiz will include practice problems to help you apply. Web the angle bisectors worksheet works at ks3 and ks4 and can be completed independently by the learner or as part of your lesson.

Web angle bisector theorem states that the bisector of any angle will divide the opposite side in the ratio of the sides containing the angle. Web an angle bisector is a straight line drawn from the vertex of a triangle to its opposite side in such a way, that it divides the angle into two equal or congruent angles. Add both of these angles together to get the whole angle.

If A Point Is In The Interior Of An Angle And Equidistant From The Sides, Then It Lies On The Bisector Of That Angle.

Multiply each side by 6. Web an angle bisector of an angle of a triangle divides the opposite side in two segments that are. The table below shows the statements related to internal and external angle bisector theorems as well as their converse. This principle is illustrated using a diagram with a yellow and green segment.

A And B Are The Lengths Of The Other Two Sides.

Since ad is the angle bisector of ∠a, by angle bisector theorem, bd/dc = ab/ac. Before attempting this sheet, pupils should know how to draw and measure angles using a protractor. Since the angle bisector cuts the angle in half, the other half must also measure 55°. These segments have equal lengths.

If A Ray Bisects An Angle Of A Triangle, Then It Divides The Opposite Side Of The Triangle Into Segments That Are Proportional To The Other Two Sides.

When we construct angle bisectors for the angles of a triangle, they meet in one point. Web the angle bisector theorem, a mathematical principle, states that any point on a bisector must be equal to each angle it cuts. By the angle bisector theorem. This principle is illustrated using a diagram with a yellow and green segment.

Find Bz, Cu, Uz, Bu.

Web help your students prepare for their maths gcse with this free angle bisector worksheet of 30 + questions and answers. Add both of these angles together to get the whole angle. Before attempting this sheet, pupils should know how to draw and measure angles using a protractor. Here, in $\delta abc$, the line ad is the angle bisector of $\angle a$.

If bd−→− b d → is an angle bisector, find ∠adb ∠ a d b & ∠adc ∠ a d c. Round to one decimal place. The quiz will include practice problems to help you apply. Ad bisects the side bc in two parts, c and d. So, rs = 6x − 5 = 6(5) − 5 = 25.